Parabolas & Culture

Ok, this thing is huge....Don't click the link to the full post unless you really, really, really mean it.

After reviewing “The Archimedes Codex” recently, I got to thinking more about how Greek mathematics differed from our own system. Specifically, I wondered about the capabilities of the two systems and how it affected certain types of calculations. Full post compares modern methods with "the Greek way", specifically for various areas under and inside parabolas.....

Warning! Full post contains mathematics (mainly calculus with a little bit of geometry)
Warning2! I am NOT an expert in Ancient Greek society or mathematics. I make many generalizations about both. I could be wrong....

Archimedes developed this geometric derivation of the area of a parabola (starts on pg10 of the pdf). The use of geometry is unsurprising as most Greek mathematics favored geometry. Not to mention, for this proof Archimedes made large use of the lever principle (which he developed) and balancing of a triangle (which he also developed)....This is known as playing to ones’ strengths.

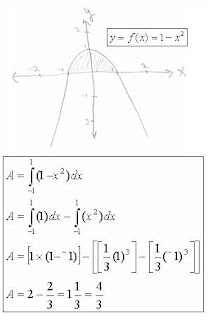
But I think it’s interesting to compare this method with how we would make the same exact calculation. Here’s my calculation of the area of a “basic” parabola:



There are several features to note about this calculation. Unlike Archimedes, our system describes the parabola with an equation not an arc (ABC). We go to great trouble to place the parabola in the correct location in space (“space” described by another modern concept, the Cartesian coordinate system). Greeks were also concerned about location but mainly in relation to shapes inscribed or circumscribed by the parabola in question. These relationships usually provided them with the identities and equivalences that allowed for complicated derivations. Also, look at the number of abstract concepts & symbols involved in the modern calculation which you have to understand in order to follow the solution: the integral sign, the equation and several theorems involving using substitutions to solve the integral.

Even though the system is very different from his method, this does correspond to Archimedes solution.


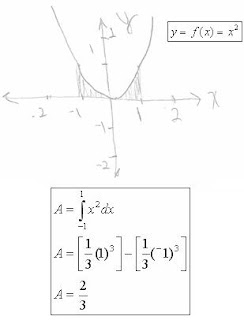
Where things begin to get interesting is when you consider the area underneath a parabola curve. There are a number of real-world problems involving these type of solution in physics but they were unheard of in Archimedes’ time.

First let’s look at how we would solve this problem:


It’s not too different from the first solution is it? And the solution is pretty easy to verify:


For both the area under the curve and the area inside the curve, we use Archimedes solution to check our own. In his day, these solutions were cutting edge thought. After two thousand years, we take them as bald facts whose origin is of no more interest to most students than the secret history of 2+2=4.

But what happens when we only want to calculate the area of a small slice underneath the parabola? For the modern system, it’s not too different than our other solutions:


However, I have no idea how or even if Archimedes would have calculated this. I attempted to recreate his parabola area figure and modified it as I felt appropriate for calculating a slice:


The problem with attempting to solve this geometrically is that there are too many variables and no clear way to relate them to each other. When looking at the curve as a whole, it’s easy to develop proportions to use in eliminating some variables. When looking for the area of a small slice, those proportions are no longer true. The relationship between what’s inside the parabola and what’s outside it changes depending on which slice you take. For instance:


There are a couple of reasons why I don’t think Archimedes or any Greek mathematician would have ever performed this calculation.

Mainly, this calculation involves ugly proportions and the Greek placed real value on “beautiful” relationships between numbers. Hence, they developed ideas such as “The Golden Spiral” and "The Golden Ratio". In general, the Greeks weren't interested in randomly-sized bits of things. They could and did manipulate proportionate pieces of whole objects. And based on Archimedes geometric calculation of the area of a parabola, they had no problem using small-bits of shapes as long as they were used to derive relationships between whole shapes. A random bit by itself had no interest.

Also, the Greeks had a much higher expectation of order in things than we do. In modern times, developments like Thermodynamics, Quantum Mechanics and Chaos Mathematics have led to a much less cultural expectation of order in the Universe (or at least much less expectation of "simple" order). Therefore, to the Greeks, to expect random slices of things to have any real-world meaning would be a little bit nuts.

I can’t even imagine a Greek mathematician sending this problem out as unsolvable. While Archimedes apparently liked to tease his competitors/colleagues, he thrived on his reputation as a master. I don’t really see him or any Greek mathematician sending a problem out stating “I couldn’t solve this” even if it was also to say “Here’s a frustrating little riddle that should keep your chickpea-sized intellect busy for a while”. Not to mention that Greek mathematicians were usually subsidized by rulers who kept them around because they could solve problems. If word got out they were stumped, it might hurt not just their prestige but their livelihoods. In Archimedes’ case, his patron was possibly his relative, Heiro II of Syracuse who made active use of Archimedes’ reputation for both military and diplomatic purposes. I don’t see any such ruler as being understanding about a drop in that reputation.

Still, before reading “The Archimedes Codex” most experts on Greek mathematics would have said Greeks also stayed away from infinities because they didn’t conform to their ideas about how numbers should work. We now know this to be untrue. It’s possible they tried other things as well and records of those calculations didn’t survive into the modern era.

If someone back then did give these bounded problems a shot, I would expect they focused on special cases which happen to have proportional relationships to the whole curve solution in order to get the variables to work out right. Also, if they sent it out to other mathematicians, I could see someone like Archimedes, knowing damn well their solution is special-case, saying “I leave the calculation of similar slices as an exercise for you.” This would allow them to present their solution (and intellect) while also teasing their competitors with a problem they would find exceedingly frustrating.

A slightly tangential point: Doesn’t the modern way strike you as almost terse and quite dense compared to the Greek methods? Their ways involve much more flourish and explicit delineation of concepts. The latter partly because they were the first to develop certain concepts so they had to explicitly delineate them. Our way really reflects our societies values of efficiency and “getting as much bang for your buck”. Each symbol represents not just itself but a whole body of thought. Each manipulation of those symbols portrays the results of hundreds of years of mathematical development.

This reminds me of a comment one of my English teachers once made that “poetry was compressed speech” where one word represented dozens so that the information provided in a poem was much larger than you would expect based on a word count. If this is true for words, I would expect it’s true of mathematics as well. It functions as a form of symbolic poetry where each symbol can express many things simultaneously. This has nothing to do with Greek mathematics specifically; I just think it’s cool.